To prove that the Earth is flat, we also have to disprove that the Earth is spherical. What we will do is take the standard model of the spherical Earth,
calculate what we expect to see, then compare the result with what is observed. If they don't agree, then the Earth is not the standard sphere that
is claimed.
[If you wish to avoid all the diagrams and calculations, please scroll to the Conclusion and
the Appendix at the end of the article which
shows two images that give absolute proof that the Earth is not flat.]
First, some key points about the video, some of which raise
a few questions:
Last Updated: 3. January 2022
Behold, your NOT flat earth
A.M.P, J.T. and A.S
A video has been posted on YouTube that claims to show irrefutable proof that the earth
is flat and ends by saying, "Behold, your flat Earth."
Compared to many flat earth videos and claims, this video is very convincing and shows some very impressive photography.
Images shown are taken from Malibu in California, USA and show highly zoomed in views, using infrared light of Mt. San Jacinto which is about 189Km
distant. It is quite amazing that this is possible.
The claim (11m08s; 11m18s) in the video is that this would be impossible to see unless the Earth was flat. The video shows a diagram that correctly
shows the elevation angle to the summit from the observation point, if the Earth was flat. The diagram shows this elevation to be 17 mrad (which
is 0.017 * 180/PI = 0.974 degrees), approximately twice the angular diameter of the sun.
Another view has a graduated scale showing this angle superimposed, apparently supporting the measurement, therefore concluding that the Earth is flat.

BUT...
- The altitude of the observation is sufficiently high to avoid questionable atmospheric effects and distortions close to the water surface as seen in many other videos.
- The optical quality of the equipment is very good with lens distortion unlikely.
- The film uses the Google Earth program which is based on a spherical Earth. Should that be used when arguing for a flat Earth?
- The observer does not give his precise position so we can't immediately test distances and angles.
- When showing the angular height of Mt. Jacinto, there is no clear demonstration of how the angle was calculated - only floor heights of a distant building were used.
- There is no indication of where the horizon is.
- The baseline used for the angular elevation of Mt. Jacinto is the shoreline - this is not the horizon and is a considerable error.
To calculate what we expect to see using the spherical Earth, refer to the diagram below:
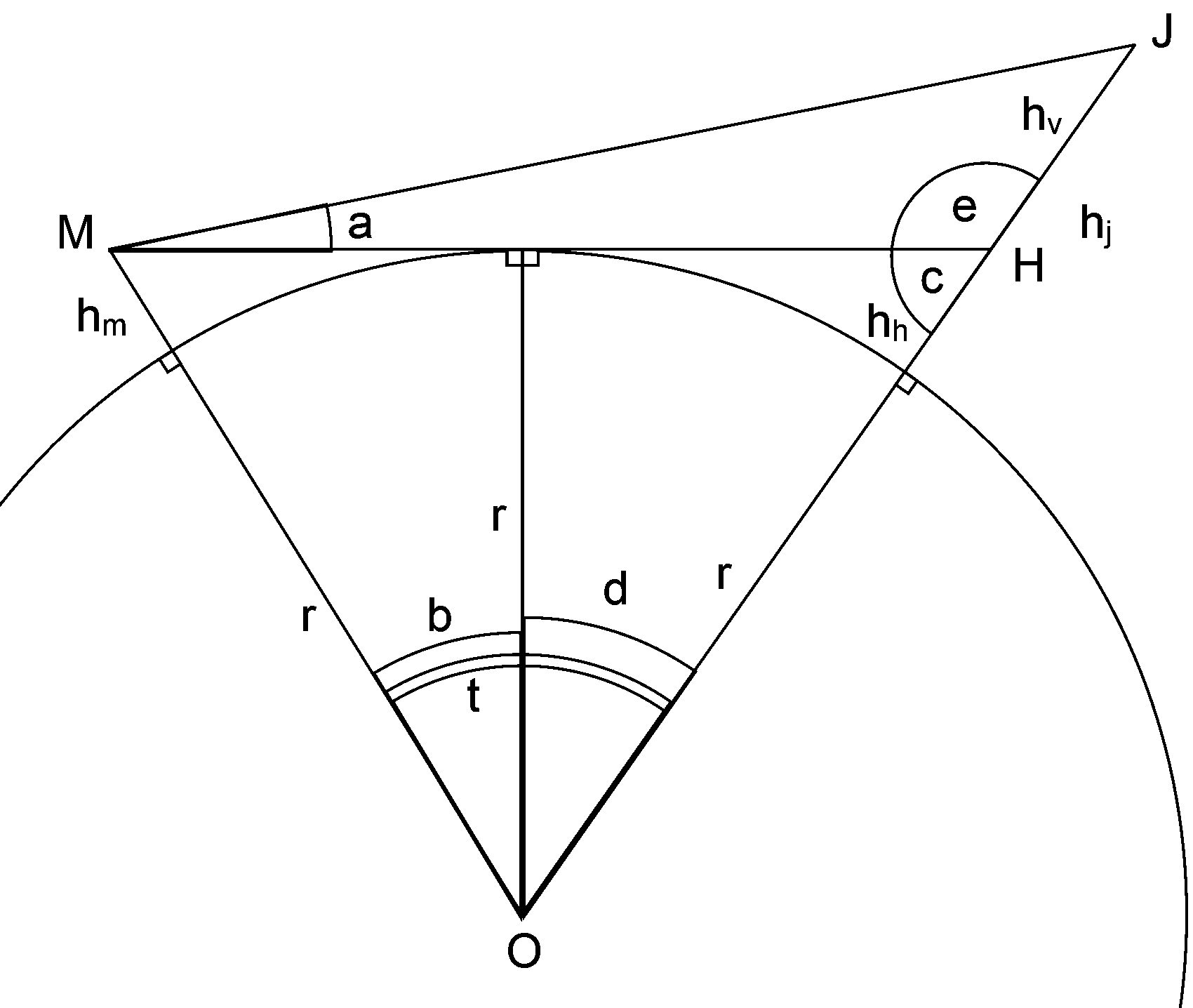
In this diagram:
| M | The location of the observation (camera) | |
| J | The summit of Mt. San Jacinto | |
| O | The center of the Earth | |
| MH | The horizon line | |
| J | The summit of Mt. San Jacinto | |
| hm | The height of the observer/camera above sea level | |
| hj | The height of Mt. San Jacinto above sea level | |
| hv | The height of the visible part of Mt. San Jacinto above the horizon (measured at the mountain). | |
| hh | The height of the hidden part of Mt. San Jacinto below the horizon. | |
| r | The radius of Earth, standard value: 6378100m. | |
| t | The angle between the observer and Mt. Jacinto. | |
| a | The angle above the horizon the observer sees the summit of Mt. Jacinto. | |
| b | The angle between the observer and the horizon. | |
| d | The angle between Mt. Jacinto and the horizon. | |
| c,e | Angles needed for calculations. |
| The approximate radius of a spherical Earth was measured by Eratosthenes in roughly 240BC. His estimate was 6316Km. |
As mentioned before, we know the location of Mt. San Jacinto, but we do not know the from where location the video was taken. However, there are some clues
in the video and searching the coastline around Malibu using the Google Earth program it is possible to come up with a reasonable estimated as shown below.
This estimate will be tested later.



The Google Earth image shows an estimate of where the Mt. Jacinto video was taken from. In the colour image
from the video, the key identification points are the fence on the left, the path, the large bush and the buildings on the beach. The fence is part of a
baseball park at Malibu Bluffs. The black and white infrared image is taken nearby with the trail on the right being the lower path in
the Google Earth image. Even the dumpsters are visible. This gives a high level of confidence that this
is the correct location.
We now have two locations to work with. (Values are taken from Google Earth.)
We now have two locations to work with. (Values are taken from Google Earth.)
| Place | Diagram | Latitude (Deg) | Longitude (Deg) | Height (m) |
|---|---|---|---|---|
| Mt. San Jacinto Summit | M | 33.814742 | -116.679402 | 3296 |
| Observer/camera Location | J | 34.032970 | -118.703468 | 61 |
Now for the calculations. What we ultimately want to find are the two heights hv and and hh, and the angle a.
1. Calculate the angle t using spherical triangle trigonometry as shown in the diagram below:

| k = 90 - 34.032970 | 55.967030 Deg |
| l = 90 - 33.814742 | 56.185258 Deg |
| x = -116.679402 - -118.703468 | 2.024066 Deg |
| t = acos[ cos(k)cos(l)+sin(k)sin(l)cos(x) ] | 1.6936183897 Deg |
As a check, the sea level distance between the observer and Mt. San Jacinto is r * t * PI / 180 (angle needs to be in radians) = 188.5 Km (117.1 Miles)
which is consistent with what is in the video.
2. Calculate angle b, the angle between the observer, the center of the Earth and the horizon.
b = acos[ r / ( r + hm ) ] = 0.2505850487 Deg
3. Calculate the angle d which is the angle between the horizon, the center of the Earth and the visible summit of Mt. San Jacinto.
d = t - b = 1.443033341 Deg
4. Now the amount of Mt. San Jacinto below the horizon, hh, can be calculated.
cos(d) = r / (r + hh) => hh = [ r / cos( d ) ] - r = 2023.4086061809m
5. Calculate the visible height of Mt. San Jacinto above the horizon.
hv = 3296 - hh = 1272.5913938191m
This is a highly significant result. It shows that using the standard spherical Earth, roughly one third of Mt. San Jacinto should be visible
above the horizon. This completely contradicts the claims made in the video that Mt. San Jacinto should not be visible.
These vallues can be cross checked with the Earth Curvature Calculator. Can we verify this using the video? Let's see. To do this we need to find angle a.
These vallues can be cross checked with the Earth Curvature Calculator. Can we verify this using the video? Let's see. To do this we need to find angle a.
6. Calculate angle c.
c = 180 - 90 - d = 88.556966659 Deg
7. Calculate angle e.
e = 180 - c = 91.443033341
8. Calculate the horizon distance MH.
MH = SQRT[ ( r + hm )^2 + r^2 ] + SQRT[ ( r + hh )^2 + r^2 ] = 188565.794500343m
9. Calculate the line of sight distance from the observer to the summit of Mt. San Jacinto, MJ. (Law of Cosines).
MJ = SQRT[ MH^2 + hv^2 - 2 * MJ * hv * cos(e) ] = 188602.132921632m
10. Calculate the elevation angle (angle above horizon, NOT horizontal), a, to the summit of Mt. San Jacinto
as viewed buy the observer. (Law of Sines).
a = asin[ hv * sin(e) / MJ ] = 0.3864831398 Deg
This angle is less than half the angle of 0.974 Deg (0.017 Rad) shown in the video, so which one is correct? At certain times, it would be possible to
observe the sunrise over Mt. San Jacinto and since the diameter of the sun is about 0.5 degrees, it would be easy to tell which of the two angles is
correct, but this is somewhat impractical.
There is another possibility and that is to use an image from the video. The camera can be used as a photogrammetric measuring device if calibrated, that is, being able to convert between image pixels and real world angles. Fortunately, the image below contains some distinctive buildings that can be identified in the Google Earth program. The angle between two of them can be calculated and the number of pixels in the image between them can be counted. This will give a scale between angles and pixels so that the angles can be shown on the image or measured from the image.
There is another possibility and that is to use an image from the video. The camera can be used as a photogrammetric measuring device if calibrated, that is, being able to convert between image pixels and real world angles. Fortunately, the image below contains some distinctive buildings that can be identified in the Google Earth program. The angle between two of them can be calculated and the number of pixels in the image between them can be counted. This will give a scale between angles and pixels so that the angles can be shown on the image or measured from the image.

Here, A, B and C are buildings that can be identified in Google Earth and the lines have been placed
on specific parts of the buildings. Building C is not necessary but almost lines up with J, the summit of Mt. San Jacinto. This provides a quick
check on the estimate of the camera position. The horizontal magenta line is the visible height of the summit. Below is the corresponding
Google Earth image showing the same buildings. A feature of
Google Earth is that markers can be placed and the coordinates of the markers read. The red line is
the line joining the observer to the summit of Mt. San Jacinto.

Using Google Earth, we obtain the following coordinates:
| Building | Latitude | Longitude |
|---|---|---|
| A | 34.011040 | -118.497544 |
| B | 34.016996 | -118.500625 |
| (C) | 34.011012 | -118.485107 |
With these coordinates and with the observation coordinates, it is possible to calculate the bearing of the buildings from the observer using
the spherical triangle diagram above. This is the angle b. Firstly, we need to calculate the angular distance as we did with Mt. San Jacinto
to get the angle t.
sin(b) / sin(l) = sin(x) / sin(t) => b = asin[ sin(l) * sin(x) / sin(t) ]
| Object | k | l | x | t | b |
|---|---|---|---|---|---|
| Building A | 55.967030 | 55.988960 | 0.205924 | 0.172077592 | 97.2642119509 |
| Building B | 55.967030 | 55.983004 | 0.202843 | 0.1688721707 | 95.3710947949 |
| (Building C) | 55.967030 | 55.988988 | 0.218361 | 0.1823097356 | 96.8565942534 |
| Mt. San Jacinto | 55.967030 | 55.988988 | 2.024066 | 0.1823097356 | 96.8375806261 |
Now calculate the scaling between the observed horizontal angles and the image pixels.
The angle between Building A and Building B is 97.2642119509 - 95.3710947949 = 1.893117156 Degrees.The horizontal distance on the image is 307 pixels which corresponds to: 162.1664031869 pixels / degree.
It is now possible to draw the horizon on the image as we know the angle between the horizon and the summit of Mt. San Jacinto, a.
Horizon distance from J = 0.3864831398 * 162.1664031869 = 62.7 pixels.
This can now be drawn on the image. The magenta rectangle 'hanging' from the summit of Mt. San Jacinto is 63 pixels high so the horizon can
be drawn from the bottom of that rectangle.

What is significant here is that the position of the horizon line has been calculated using the maths above and is entirely consistent with what is
expected. The blue rectangle represents the angle given in the video, and is also the full height of Mt. San Jacinto. Its base is clearly below
the horizon so the claim made in the video is incorrect. (The base should be on the horizon).
Now, if the surface of the Earth is curved, the horizon will always be lower than eye level. Using some of the dimensions in the first diagram, we
can draw this one which shows the eye level position in relation to the summit of Mt. San Jacinto. This is the angle s.

Using the Law of Sines,
( r + hj ) / sin( s + 90 ) = MJ / sin( t ) => sin( s + 90 ) = ( r + hj) * sin( t ) / MJ
=> s = 0.134600958 Deg
This corresponds to 0.134600958 * 162.1664031869 = 21.8 pixels
In the picture above, the cyan rectangle 'hanging' from summit of Mt. San Jacinto is 22 pixels high. The line connected to the bottom of it represents
the eye level of the observer/camera in Malibu. This could be confirmed with survey equipment making sure that the observing device is horizontal.
A point to note is that the line is above the magenta horizon line which is the consistent with a spherical Earth. This looks quite a large difference
in this image but that is because it is highly magnified. The difference is about half the diameter of the Sun.
As a final check on the estimated camera position, we can now plot on the image the calculated horizontal positions of Building A and Building B and
compare them with the actual positions.
For Building A, the number of pixels to the right of Mt. San Jacinto is
162.1664031869 * ( 97.2642119509 - 96.8375806261 ) = 69.2 pixels (right)
For Building B, the number of pixels to the left of Mt. San Jacinto is
162.1664031869 * ( 96.8375806261 - 95.3710947949 ) = 237.8 pixels (left)
These have been drawn as the orange rectangles on the image below.

This shows a remarkable agreement between the observations and calculations, showing that the estimated camera position was very close actual camera position.
The fact that the error is the same for both buildings (slighty to the right) shows just how close the observed and calculated values are. The real
camera location is slightly to the left of the estimated position.
Conclusion
The video used for this article uses some very good quality images to show long distance views of Mt. San Jacinto from Malibu Bluffs. The claim
is made that it would only be possible to see Mt. San Jacinto at this large distance if the Earth was flat and not if the Earth was the generally accepted
sphere. However, using the standard spherical Earth model and standard trigonometry, this article has demonstrated that what is seen in the video is
exactly what would be expected if the Earth was a sphere of standard radius.
The images used in this video prove absolutely and without any doubt, that the Earth is not flat.
Appendix
A very simple way of showing that the claims of a flat Earth in the video are in error is to simply see how much of Mt. San Jacinto is actually visible. Here
the town of Hemet is very useful as it is near the base of Mt. San Jacinto and viewing angle is fairly similar to the video.

Hemet lies between 450m and 500m above sea level so in the image below we are seeing the top 2800m of Mt. San Jacinto.

Note particularly the snow covered top part and you can see the snow comes down to the shoulders on either side. Now look at the composite image
taken from the YouTube video:

It is quite clear that the top part of Mt. San Jacinto appears very similar in both images since both observation angles are not very different. The
shoulders are just visible above the much closer ridge of hills (about 100m high). What should be strikingly obvious from the video image is that
we are only seeing the very top part of Mt. San Jacinto. Even allowing for the part obscured by the coast, if the Earth was flat, virtually all of
what is visible from Hemet should be visible in this image. Clearly it is not. These two images are simple visual proof that the Earth is not flat.
Just as a final demonstration, here are the two images placed side by side. Notice how much of Mt. San Jacinto should be visible from Malibu if the Earth was flat.
Just as a final demonstration, here are the two images placed side by side. Notice how much of Mt. San Jacinto should be visible from Malibu if the Earth was flat.
 "...you see indeed, but don't perceive.' - Isaiah 6:9
Behold, your NOT flat Earth
"...you see indeed, but don't perceive.' - Isaiah 6:9
Behold, your NOT flat Earth