Absolute Simple Proof that the Earth is Round

In recent times there has been an increase in the number of people claiming that the earth is flat.

However, what follows is a simple absolute proof that the earth is spherical without needing difficult science or complex maths.
This is a simple observation that anyone can make although it does require travelling to different parts of the earth.
Alternatively, other observers in different places could be asked about what they can see.

This observation requires measuring the angle above the horizon of the star Polaris (Alpha Ursa Minor) from different latitudes.

An important point about this observation is that Polaris is sufficiently far away, to consider that light rays from it are parallel when they reach the earth. Just as two people standing a couple of meters apart from each other will see Polaris in exactly the same part of the sky.
(If you want to be technical, look up parallax).

Polaris is a useful star because it is almost aligned* with the earth's rotational axis so that it appears almost directly overhead for an observer standing at the North Pole. Flat earthers and round earthers would agree on this.

Let us consider an observer standing at the North Pole and making a journey south. Does the observer see Polaris in a different part of the sky when they travel, and if so, how far has it moved?

For the round earth, look at the following diagram:

The observer starts at n with Polaris, p directly overhead. The observer makes an obsevation at three places: a third of the way to the equator at h, two thirds of the way to the equator at c and on the equator itself at e. The observations are made at equal intervals of 30 degrees latitude.

The diagram on the right shows how far Polaris appears above the horizon when looking due north as viewed from these different locations.
In the diagram on the left, the observer's local horizon is shown as the short dotted line.
When at h, the observer's latitude is 60 degrees north and Polaris appears 60 degrees above the horizon.

This is exactly what is observed in reality. The angle Polaris makes above the northern horizon, is the same as the observer's latitude. This is what makes Polaris a useful navigation guide. Go and try it yourself!

What is really important to note here is that when moving south by equal distances ( n to h, h to c, c to e) the change in elevation of Polaris will also change by equal angles, in this example: 30 degrees, 30 degrees and 30 degees.

THIS IS OBSERVABLE AND CAN ONLY HAPPEN ON A ROUND EARTH.

In this diagram the positions represent real places: n is the North Pole, h is Helsinki, Finland, c is Cairo, Egypt and e is Entebbe, Uganda.
Also, look at the observer at d (Dunedin, New Zealand). Here, Polaris is below the local horizon. It is below the horizon anywhere south of the Equator and hence not visible.** Again, this only can happen with a round earth.

Now, let us see what happens if the earth is flat. Using this diagram:

This is a scale drawing.
The flat earth model generally puts the sun at 5000Km[1] above the surface of the earth. The stars are beyond the sun but for this demonstration, we will start by placing Polaris at the same height of 5000Km above the earth, and see what happens.
Just as in the round earth case, an observer at n will see Polaris over head.
Unlike the round earth example, a flat earth can not use angles when heading south, only distances can be used. These will be the same as those used for the round earth with the North Pole to Equator distance being very close to 10000Km. So, the distance between n and h is 3333Km, as is the distance between h and c, and, c and e. The distance from North Pole to the southern edge is 20000Km.

What should be possible to see here is that the differences in the angles w, x, y, and z are not the same.
In the round earth model, the differences are all the same and equal 30 degrees.
What is observed in reality is the round earth case.

THIS PROVES THE EARTH IS NOT FLAT.

Placing Polaris further away does not change this. The only time when the differences in the angles are the same is when Polaris is placed sufficiently far away that the light rays from it are parallel, in which case, Polaris would appear over head in every location. This is simply not observed.
Note also that in the flat earth model, an observer at the southern rim, s, can also see Polaris, however, in reality, Polaris is not observable south of the Equator.

THIS ALSO PROVES THE EARTH IS NOT FLAT.

Flat earthers: Please use the eyes that God gave you!

Some Numbers

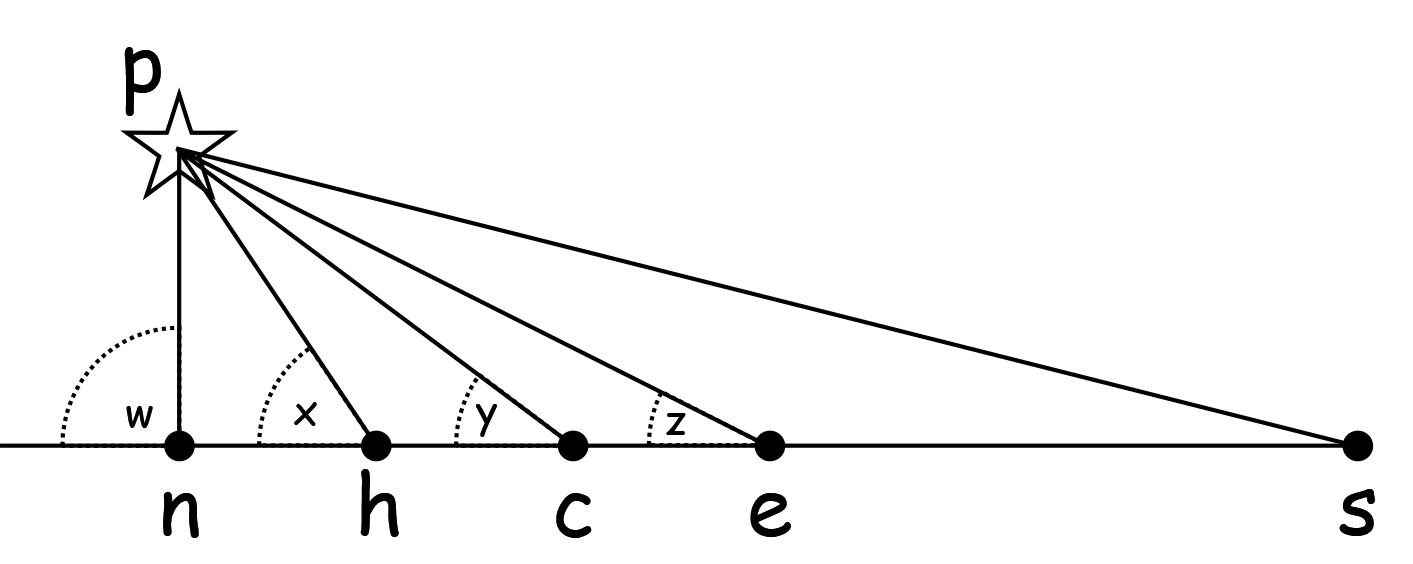
Location	n	h	c	e	s	n-h	h-c	c-e
Distance from n(Km)	0	3333	6667	10000	20000
	w	x	y	z	(s)	w-x	x-y	y-z
Round Earth Angles
	90.0	60.0	30.0	00.0		30.0	30.0	30.0
Flat Earth Angles
Distance to Polaris: 5000Km	90.0	56.3	36.9	26.6	14.0	33.7	19.4	10.3
Distance to Polaris: 8000Km	90.0	67.4	50.2	38.7	21.8	22.6	17.2	11.5
Distance to Polaris: 10000Km	90.0	71.6	56.3	45.0	26.6	18.4	15.3	11.3
Distance to Polaris: 100000Km	90.0	88.1	86.2	84.3	78.7	1.9	1.9	1.9
Distance to Polaris: 1000000Km	90.0	89.8	89.6	89.4	88.9	0.2	0.2	0.2
Distance to Polaris: 10000000Km	90.0	89.9	89.9	89.9	89.9	0.0	0.0	0.0

Note here that with Polaris only a million Km from n, the light rays reaching the flat earth are almost parallel and all observers will see Polaris over head - which is definitely not observed in reality.

Some Technical Stuff

* Polaris is not exactly over the North Pole but lies about three quarters of a degree away - that is one and a half moon diameters. The numbers used above have assumed Polaris to be directly over the North Pole so real measured observations could be out by 0.75 degrees.

** Actually, if the atmosphere is perfectly clear it is still possible to see stars that are just below the horizon because the atmosphere bends (refracts) the light by roughly half a degree (one moon diameter). So, with the slight misalignment of Polaris and with perfect seeing conditions it may be possible, at certain times, to observe Polaris from about a degree south of the Equator.

The latitudes of the listed cities are not exactly 60, 30, and 0 degrees.

The angles calculated in the flat earth case use the simple trigonometry of the right-angled triangle using the following equation:

   Elevation of Polaris = arctan( <altitude of Polaris> / <Distance from n> )

On the Windows calculator, make sure it is set to degrees (not Radians), enter the altitude, enter /, enter the distance, enter Inv, enter Tan, and the answer appears.
If using a spreadsheet, it may be necessary to convert the answer to degrees by multiplying by Pi (3.14159) and dividing by 180.

20. Apr 2018